警告
本文最后更新于 2020-09-03,文中内容可能已过时。
在真实的世界中,很多问题是不存在快速解法的,只能穷尽搜索,因此一个高效的搜索技术非常重要。回溯(Backtracking)和分支限界(Branch&Bound)就是两种减小搜索空间大小的技术。
1. 回溯的基本思想
1.1 解空间树
假设可以用一个 n 元组 $X=(x_1,x_2,……,x_n)$ 来表示所求问题的解,其中 $x_i$ 的取值范围为某个有穷集合 S。我们把 $X=(x_1,x_2,……,x_n)$ 所有可能取值的组合称作问题的解空间。
举个例子,假设 0-1 背包问题中物品有 3 个,用 $X=(x_1,x_2,x_3)$ 表示,其中 $x_i \in \{0,1\}, 1 \leq i \leq 3$,则问题的解空间为 $\{(0,0,0),(0,1,0),(0,0,1),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)\}$
我们用一颗 n+1 层的树来表示解空间,其中,第 i 层和第 i+1 层之间边的标号表示变量 $x_{i+1}$ 的可能取值,从根结点到叶节点路径上的标号就构成问题的一个可能的解。
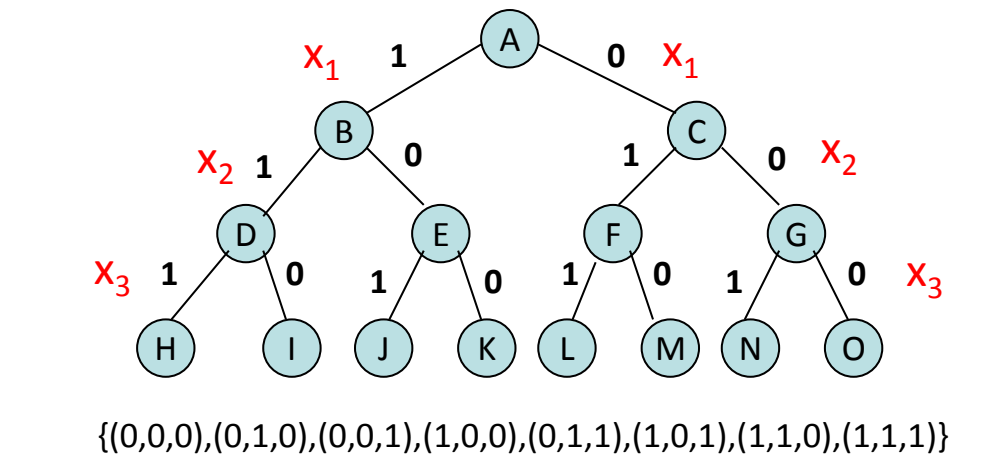
我们还可以这样理解解空间,将解空间划分为两个维度:一个可行解中元素的个数和每个元素的取值范围。这两者正好对应解空间树的深度(实际是深度-1)和宽度。比如在上面的 0-1 背包问题中,问题的一个解由一个 3 元组 $X=(x_1,x_2,x_3)$ 表示,这里每个解中有 3 个元素,因此解空间树的深度是 4,每个元素有 0 和 1 两个取值,因此每个节点有两棵子树。
注:这里树的深和宽不是标准化的说法,仅为了便于说明。理解上面这段话非常有利于实际解决问题时解空间树的构造。
1.2 基本思想
回溯的基本思想是:在问题的解空间树中,按照深度优先的策略,从根结点出发搜索。搜索至任一结点时,先判断该结点和其儿子结点的边所标记的值是否满足解的要求,是就加入到解中,继续向下深度优先搜索以其儿子结点为根的子树,否则就结束对以该儿子结点为根的子树的搜索,选择对另一个儿子结点作为根的子树进行搜索。全部搜索完毕或都不满足就向父节点回溯。
仍以 0-1背包问题为例,设物品重量为 $w=[16,15,15]$,物品价值为 $v=[45,25,25]$,背包容量 $c=30$。定义 $r$ 为当前背包的剩余容量,$v$ 为当前背包的价值。因为物品有 3 个,所以树深为 3+1=4,又因为每个解元素有两种取值,1为放入背包,0为不放入,所以每个结点有两棵子树,最终解空间树绘制如下
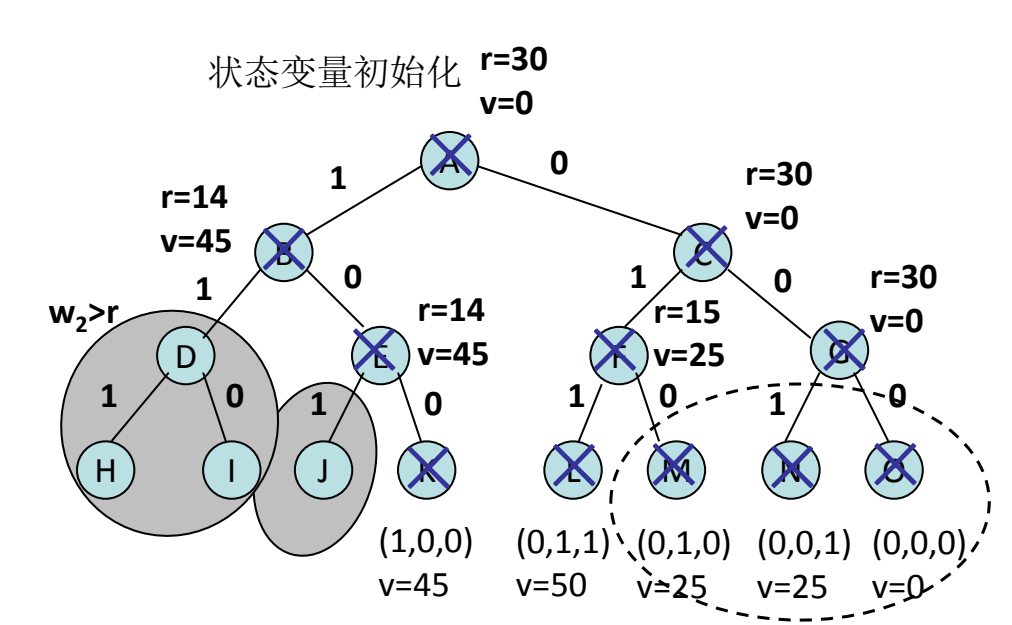
遇到某个结点判断与儿子结点的边是否满足条件时,用到剪枝函数,分两种
- 约束函数:就是不可行的解,比如上图第二层第一个结点,r=14,小于当前物品重量 15,因此子树不可行;
- 限界函数:就是非最优解,比如上图虚线框起来的结点,因为之前得到的最大价值为 v=50,这里出现的 v 都小于该值,所以不是最优解。
我们理解了基本思想后,就可以很容易的发现回溯的最坏时间复杂度是 $O(N×2^N)$
1.3 一般步骤
回溯法的一般步骤为
- 针对所给问题,定义问题解空间
- 确定易于搜索的解空间树
- 以深度优先的方式搜索解空间树,并在搜索过程中用剪枝函数避免无效搜索
- 用约束函数考察左子树是否可行
- 用限界函数考察右子树是否(有可能)最优
经常用回溯法解决的问题有两类:子集树和排列树。子集树是从 n 个元素的集合中找出满足某种性质的子集,排列树是确定 n 个元素满足某种性质的排列,下面分别介绍两类问题的思路。
2. 子集树
给定一个不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。leetcode 78题-子集
注:解集不能包含重复的子集
1
2
3
4
5
6
7
8
9
10
11
12
| 示例输入: nums = [1,2,3]
示例输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
|
回溯法可以保证生成的结果完整无冗余,实际上,就是输出整棵子集树(解空间树)。本题中,解向量的维度是 3 ,每个解元素有选择和不选择两种可能,因此解空间树是一颗4层的二叉树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| func subsets(nums []int) [][]int {
res := make([][]int,0)
cur := make([]int,0)
// 使用闭包可以节省 nums,res,cur 三个参数的传递,同时避免 res 的全局定义
// 必须事先声明,否则无法在函数中调用自身
var backTrace func(level int)
// 回溯的思路是每个元素都有选择与不选择两种可能,解空间树是一棵 n+1 层二叉树
backTrace = func(level int) {
// len(nums)+1 层说明位于叶子节点,将当前可行解加入结果数组
if level > len(nums) {
// 建立一个新切片,将结果复制到新切片,然后再添加到结果集,因为 cur 是指向结果的指针,指向的结果后面还会变动
tmp := make([]int,len(cur))
copy(tmp,cur)
res = append(res,tmp)
return
}
// 遍历二叉树的两个分叉
for i := 0; i <= 1; i++ {
// i 为 0 表示当前元素不加入当前解
if i == 0 {
backTrace(level+1)
}else{
cur = append(cur,nums[level-1])
backTrace(level+1)
// 删除当前元素然后进行回溯
cur = cur[:len(cur)-1]
}
}
}
backTrace(1)
return res
}
|
一种常用的减小时空复杂度的方法是位运算,用于每个元素的可能取值为 0 和 1 的情况。取值只有 0 和 1 的情况下,我们可以将一条完整的路径看作一个二进制数字,比如一个 n+1 层的二叉树的每一个可行解都可以看作一个 n+1 位的二进制数字,二进制数字的每一位代表该层的元素选择或不选择,这样,只要生成所有可能的二进制数就构成了一个完整的解空间,程序如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| func subsets(nums []int) [][]int {
ln := len(nums)
// 这样移位保证左边0的存在,比如一共3位,保证001而不是0,可以从 1000 到 10000 进行遍历,取每个值的右边三位
s, e := 1<<ln, 1<<(ln+1)
var res [][]int
for i := s; i < e; i++ {
var tmp []int
for j := 0; j < ln; j++ {
// 通过与运算判断当前位是否为1,为1则加入结果,i为当前元素
if i&(1<<j) != 0 {
tmp = append(tmp, nums[j])
}
}
res = append(res, tmp)
}
return res
}
|
上面的子集树问题还有另一种回溯思路,那就是单独计算每一种可能长度的解的集合,然后统一添加到最终的集合。比如对于 nums=[1,2,3],一个元素的解集为{[1],[2],[3]},两个元素的解集为{[1,2],[2,3],[1,3]},三个元素的解集为{[1,2,3]},再加上空集,就是总的结果。程序如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| func subsets(nums []int) [][]int {
res := make([][]int,0)
// 使用闭包可以节省 nums 和 res 两个参数的传递,同时避免 res 的全局定义
var backTrace func(cur []int, index,length int) // 必须事先声明,否则无法在函数中调用自身
backTrace = func(cur []int, index,length int) {
// 结束条件为元素个数达到了当前限定的长度
if len(cur) == length {
// 将结果复制到新切片后再添加到结果集,因为 cur 是指向结果的指针,指向的结果后面还会变动
tmp := make([]int,length)
copy(tmp,cur)
res = append(res,tmp)
return
}
// 可以看作遍历子树,儿子节点所有可能的取值是未使用过的值,也就是索引 index 之后的值
for i := index; i < len(nums); i++ {
// 当前节点加入结果,然后递归遍历子树
cur = append(cur,nums[i])
backTrace(cur,i+1,length)
// 进行回溯,去除当前结果,回到上一层
cur = cur[:len(cur)-1]
}
}
// 对于每个长度的序列,将所有可能加入最终的结果集
for i := 0; i <= len(nums); i++ {
cur := make([]int,0)
backTrace(cur,0,i)
}
return res
}
|
用回溯法搜索子集树的一般算法为
1
2
3
4
5
6
7
8
9
10
11
12
| Backtrack(k)
//t:递归深度,即当前活动结点在解空间树中的深度,根节点t=1
//n:解空间树的高度,即问题的规模
//算法已搜索到一个叶结点,对可行解x进行记录或输出
if t > n output(x)
else
//搜索当前活动结点的子树
for i = 0 to 1 do //以二叉树为例
x[t] = i //当前活动结点x[t]的第i个取值
//满足约束条件且目标函数未越界时,搜索子树
if (Constraint(t) and Bound(t))
Backtrack(t+1)
|
如果说上面求子集的例子其实是求所有的可能,没有进行剪枝,下面可以给出另一个例子
1
2
3
4
5
6
7
8
9
10
| 题目:数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:n = 3
输出:[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
|
程序如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| func generateParenthesis(n int) []string {
res := make([]string,0)
cur := make([]byte,0)
a,b := 0,0
var backTrace func(level int)
backTrace = func(level int) {
if level > 2*n {
if a == b {
res = append(res, string(cur))
}
return
}
if a < n {
cur = append(cur,'(')
a++
backTrace(level+1)
cur = cur[:len(cur)-1]
a--
}
if b < a {
cur = append(cur,')')
b++
backTrace(level+1)
cur = cur[:len(cur)-1]
b--
}
}
backTrace(1)
return res
}
|
其中 a < n 和 b < a 就是用来剪枝的,回溯的一个关键步骤就是在调用回溯函数之前添加到结果集,之后从结果集删除,这就是回溯的本质含义。
3. 排列树
以全排列的例子开头,leetcode 64题-全排列
1
2
3
4
5
6
7
8
9
10
11
| 题目:给定一个没有重复数字的序列,返回其所有可能的全排列。
示例输入: [1,2,3]
示例输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
|
排列与子集问题的区别在于每一层子树的个数都减1,因为已选择的元素不必再次出现,因此,全排列问题是一棵4层,然后每层子树个数依次减一的树,这样时间复杂度也很容易理解,就是 $N!$。
解上面问题的程序如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| func permute(nums []int) [][]int {
res := make([][]int,0)
cur := make([]int,0)
var backTrace func(level int)
backTrace = func(level int) {
if level > len(nums) {
tmp := make([]int,len(cur))
copy(tmp,cur)
res = append(res,tmp)
return
}
for i := level-1; i < len(nums); i++ {
cur = append(cur, nums[i])
// nums 数组中,level-1 索引前的是已用过的,不能选,只能选 level-1 之后的,在未选元素
//集合中选了任何一个元素后,与未选元素集合的第一个交换,相当于把刚刚选择的元素加入了已选元
//素集合,到下一层索引向前移动一格,就保证了下一层的未选元素集合正确
nums[i],nums[level-1] = nums[level-1],nums[i]
backTrace(level+1)
cur = cur[:len(cur)-1]
nums[i],nums[level-1] = nums[level-1],nums[i]
}
}
backTrace(1)
return res
}
|
思路和子集树基本相同,多的一个步骤交换是用来处理每层子树个数减一这个问题的,实质是不断的调整未选择元素的集合。交换是一种高效的做法,除此之外,还可以用一个 Map 来标记已选和未选元素。
用回溯法搜索排列树的一般算法为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| Backtrack(k)
//t:递归深度,即当前活动结点在解空间树中的深度,根节点t=1
//n:解空间树的高度,即问题的规模
//算法已搜索到一个叶结点,对可行解x进行记录或输出
if t > n output(x)
else
//搜索当前活动结点的子树
//处理[t:n]的排列
for i = t to n do
swap(x[t],x[i])
//满足约束条件且目标函数未越界时,搜索子树
if (Constraint(t) and Bound(t))
Backtrack(t+1)
swap(x[t],x[i]) // 回溯到交换之前
|


 支付宝
支付宝 微信
微信