算法-贪心
贪心是一种策略,是一种总是寻求当前最优的策略。因为贪心只关心局部的最优,因此不是总能得到全局的最优解,所以我们选择贪心解决问题时必须保证状态的独立性,即当前最优值只与当前状态有关,不会影响以后的状态。
动态规划与贪心的区别在于动态规划状态之间是有联系的,这也是状态转移方程的制定依据,但它们也有相同之处,那就是原问题的最优解必须包含子问题的最优解,这条性质叫做最优子结构性质,这是一个问题可用动态规划或贪心来解决的基础。
下面我们通过一系列的问题来说明贪心问题,尤其要关注的是贪心策略的选取。
1. 背包问题
问题描述:给定 n 种物品和一个背包。物品 i 的重量是 $w_i$,其价值为 $v_i$,背包的容量为 c。问应如何选择装入背包 的物品,使得装入背包中物品的总价值最大?
背包问题是可用贪心来解决的,直觉上,可以有以下几种贪心选择策略
- 价值贪心:优先选择价值最大的物品,但这种方法如果选择的物品重量很大,背包载重的消耗速度会很快;
- 重量贪心:优先选择重量最小的物品,这种方法又不能保证价值快速增加;
- 价值重量比:将物品重量按单位重量的价值降序排列,依次装入,这样能保证最优。
| |
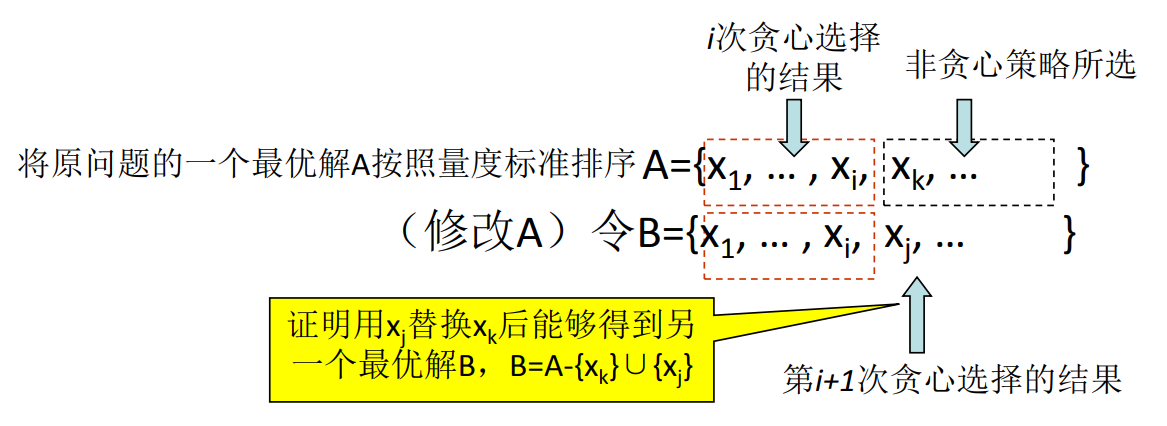
如果想要证明该问题使用贪心算法是可行的,可以按如下思路:首先证明原问题的一个最优解是以贪心选择开始。然后假设i次贪心选择能 够得到一个最优解,那么证明i+1次贪心选择也能得到一个最优解。一个图解如下
2. 活动安排问题
要求高效地安排一系列争用某一公共资源(如会议室)的活动,使尽可能多的活动能兼容使用公共资源,这就是活动安排问题。
设有 n 个活动的集合 $E={e_1 ,e_2…e_n}$,其中每个活动都要求使用同一资源,而在同一时间内只有一个活动能使用 这一资源。每个活动 i 都有一个要求使用该资源的起始 时间 $s_i$ 和一个结束时间 $f_i$,且 $s_i < f_i$。如果选择了活动 i,则它在半开时间区间 $[s_i ,f_i)$内占用资源。若区间$[s_i ,f_i)$与区间$[s_j ,f_j)$不相交,则称 $e_i$和$e_j$ 是相容的。 也就是说,当 $s_i≥f_j$ 或 $s_j≥f_i$ 时,活动 i 和活动 j 相容。
我们可以想到的贪心策略有
- 选择具有最早开始时间的活动
- 选择具有最早结束时间的活动
- 选择具有最少占用时间的活动
- 选择覆盖未选择活动最少的活动
但直观上,每次选择具有最早结束时间的相容活动,使剩余 的可安排时间段极大化,以便安排尽可能多的相容活动。事实也是如此,我们用图来说明一个实例

实现如下
| |
 支付宝
支付宝 微信
微信