警告
本文最后更新于 2020-07-04,文中内容可能已过时。
二叉搜索树是二叉树的一种特殊形式,由于它对查找的良好特性,使用较为广泛,本篇文章我们对其进行介绍,同时也包括二叉搜索树的各种进阶,比如二叉平衡树。
1. 二叉搜索树
1.1 定义
二叉搜索树(BST,Binary Search Tree),也称二叉排序树或二叉查找树。其定义如下
二叉搜索树:是一颗二叉树,可以为空,如果不为空,满足下列性质
- 非空左子树的所有结点值小于其根结点的结点值
- 非空右子树的所有结点值小于其根结点的结点值
- 左右子树都是二叉搜索树
一种最常见的题型就是判断一棵树是否为二叉搜索树,我们可以利用递归的思路来解决该问题,示例代码如下,每个节点有一次递归调用,因此时间复杂度为O(n),递归深度为树高,因此空间复杂度为O(h),h 为树高。
1
2
3
4
5
6
7
8
9
10
11
12
13
| func isValidBST(root *TreeNode) bool {
return helper(root, math.MinInt64, math.MaxInt64)
}
func helper(root *TreeNode, lower, upper int) bool {
if root == nil {
return true
}
if root.Val <= lower || root.Val >= upper {
return false
}
return helper(root.Left, lower,root.Val) && helper(root.Right, root.Val, upper)
}
|
另外,我们还应该知道,对于二叉搜索树,中序遍历可以得到一个递增的序列,所以利用中序遍历也可以进行判断。代码如下,因为完全遍历一遍,时间复杂度为O(n),栈的大小为节点数目,因此空间复杂度也为O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| func isValidBST(root *TreeNode) bool {
stack := make([]*TreeNode,0)
preNum := math.MinInt64 // 用一个变量记录上一个数,和当前值比较
for root != nil || len(stack) != 0 {
for root != nil {
stack = append(stack,root)
root = root.Left
}
if len(stack) != 0 {
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
if root.Val <= preNum {
return false
}
preNum = root.Val
root = root.Right
}
}
return true
}
|
两种写法中都要注意,二叉搜索树必须左子树的所有节点都小于当前节点值,右子树的所有节点都大于当前节点值,等于是不可以的。换句话说,序列是严格递增的。
1.2 基本操作
二叉搜索树的基本操作包括查找、插入和删除。
查找
查找的基本思路是从根结点开始,如果树为空,返回NULL,如果树非空,则将根结点的值和X进行比较,分情况处理:
- 如果X小于根结点的值,在左子树中继续搜索
- 如果X大于根结点的值,在右子树中继续搜索
- 若两者值相等,搜索完成,返回指向该结点的指针
递归的实现思路如下,空间复杂度O(h),时间复杂度O(h)
1
2
3
4
5
6
7
8
9
10
| func searchBST(root *TreeNode, val int) *TreeNode {
if root == nil || root.Val == val {
return root
}
if val < root.Val {
return searchBST(root.Left,val)
}else{
return searchBST(root.Right,val)
}
}
|
迭代的实现思路如下,空间复杂度O(1),时间复杂度O(h)
1
2
3
4
5
6
7
8
9
10
11
12
| func searchBST(root *TreeNode, val int) *TreeNode {
for root != nil {
if val < root.Val {
root = root.Left
}else if val > root.Val {
root = root.Right
}else{
return root
}
}
return nil
}
|
插入
二叉搜索树插入节点的方法是将其作为某个叶节点的子节点,核心是找到待插入的叶节点,一个递归的实现如下,时间和空间复杂度都是O(h)
1
2
3
4
5
6
7
8
9
10
11
12
13
| func insertIntoBST(root *TreeNode, val int) *TreeNode {
if root == nil {
root = &TreeNode{val, nil, nil}
}
if val > root.Val {
root.Right = insertIntoBST(root.Right, val)
} else if val < root.Val {
root.Left = insertIntoBST(root.Left, val)
}
return root
}
|
迭代的实现如下,时间复杂度为O(h),空间复杂度为O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| func insertIntoBST(root *TreeNode, val int) *TreeNode {
newNode := &TreeNode{Val:val}
cur := root
for cur != nil {
if val < cur.Val {
if cur.Left == nil {
cur.Left = newNode
return root
}else{
cur = cur.Left
}
}else if val > cur.Val {
if cur.Right == nil {
cur.Right = newNode
return root
}else{
cur = cur.Right
}
}
}
return newNode
}
|
删除
二叉树的删除比较复杂,要考虑三种情况
要删除的是叶节点,则直接删除,并修改其父结点指针为NULL

要删除的结点只有一个孩子,则将其父结点的指针指向要删除结点的孩子结点

要删除的结点有左右两颗子树,则用另一个结点替代被删除的结点,可以是右子树的最小结点,也可以是左子树的最大结点

所以删除操作会涉及两个额外的操作,查找最大和最小元素,这两个操作只需要记住两点:
- 最大元素一定在树的最右分支的端结点上
- 最小元素一定在树的最左分支的端结点上

查找最小元素的递归方法参考实现如下
1
2
3
4
5
6
7
8
| func FindMin(root *TreeNode) *TreeNode {
if root == nil
return nil
else if root->Left == nil
return root
else
return FindMin(root->Left)
}
|
查找最大元素的迭代方法参考实现如下
1
2
3
4
5
6
7
8
| func findMax(root *TreeNode) *TreeNode {
if root != nil {
for root.Right != nil {
root = root.Right
}
}
return root
}
|
最后,删除操作的参考实现如下,时间复杂度和空间复杂度都是O(h)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| func deleteNode(root *TreeNode, key int) *TreeNode {
if root == nil {
return nil
}
if key < root.Val {
root.Left = deleteNode(root.Left, key)
} else if key > root.Val {
root.Right = deleteNode(root.Right, key)
} else {
if root.Left != nil && root.Right != nil {
root.Val = findMin(root.Right).Val
root.Right = deleteNode(root.Right, root.Val)
} else {
if root.Left == nil {
root = root.Right
} else if root.Right == nil {
root = root.Left
}
}
}
return root
}
|
1.3 最近公共祖先
最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
虽然我们这里讨论二叉搜索树的最近公共祖先,但对于普通的二叉树,也有求最近公共祖先的题型,其递归解法遵循这样的思路
- 如果根结点为 nil,那么最近公共祖先为 nil
- 如果根结点等于两个节点中的任何一个,那么最近公共祖先就是根结点
- 此时我们递归调用分别求以左节点和右节点为根,针对 p,q 两个节点的最近公共祖先,如果两边返回的值都不为空,那么最近公共祖先是根结点。这里的逻辑是这样的,因为我们前面的条件中只要 p或q 任何一个节点等于根结点,就会返回,所以这一步递归调用的结果只能说明子树中包含 p 或 q,所以如果两个子树的返回值都不为空,说明 p,q 分别位于两个子树中,那么最近公共祖先是根结点;
- 这一步我们就能确定最近公共祖先不是在左子树就是在右子树,返回非空的一方即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root == nil {
return nil
}
if root.Val == p.Val || root.Val == q.Val {
return root
}
left := lowestCommonAncestor(root.Left, p, q)
right := lowestCommonAncestor(root.Right, p, q)
if left != nil && right != nil {
return root
}
if left == nil {
return right
}
return left
}
|
递归解法的时间和空间复杂度都是O(n),如果用迭代解法,其实就是遍历二叉树,然后用哈希表记录每个节点的父节点,然后遇到 p 和 q 就往祖先节点回溯,找到公共的祖先。
如果求二叉搜索树的最近公共祖先,二叉树的解法当然是适用的,但是没有充分利用二叉搜索树的特性,如果我们利用其二叉搜索树的特性,递归的思路更加简单。我们可以这样想
- 从根结点开始
- 如果节点 p 和节点 q 的值都小于根结点的值,那么最近公共祖先一定在左子树;
- 如果节点 p 和节点 q 的值都大于根结点的值,那么最近公共祖先一定在右子树。
代码如下,时间复杂度和空间复杂度都是O(h),h为树高
1
2
3
4
5
6
7
8
9
10
| func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if p.Val < root.Val && q.Val < root.Val {
return lowestCommonAncestor(root.Left,p,q)
}
if p.Val > root.Val && q.Val > root.Val {
return lowestCommonAncestor(root.Right,p,q)
}
return root
}
|
如果我们用迭代的话,还是同样的思路,但是空间复杂度可以到O(1)
1
2
3
4
5
6
7
8
9
10
11
12
| func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
for root != nil {
if p.Val < root.Val && q.Val < root.Val {
root = root.Left
}else if p.Val > root.Val && q.Val > root.Val {
root = root.Right
}else{
return root
}
}
return nil
}
|
2. 平衡二叉树
平衡二叉树(Balanced Binary Tree),它要么是一颗空树,要么满足任一结点左右子树高度差的绝对值不超过1。一般使用「平衡因子(Balance Factor, BF)」来描述这一高度差,设HL和HR分别为树T左右子树的高度,则BF满足:
$$
BF(T) = \left|H_L - H_R\right| \le 1
$$
此外,平衡二叉树的高度为$O(\log_2n)$,证明如下
设$f_n$为高度为n的AVL树所包含的最少结点数,则有
$$
f_n= \begin{cases} 1&(n=1)\ \\ 2&(n=2)\ \\ f_{n-1}+f_{n-2}+1& (n>2) \end{cases}
$$
显然$\{ f_n + 1 \}$是一个斐波那契数列,由于斐波那契数列以指数的速度增长,因此AVL树的高度为$O(\log_2n)$
注意,给定节点数,树高可能有两种情况,我们对树高和这个高度允许的节点数列表如下,
| 树高 | 节点数范围 |
|---|
| 1 | 1 |
| 2 | 2-3 |
| 3 | 4-7 |
| 4 | 7-15 |
| 5 | 12-31 |
所以给定节点数N,其高度可能是 $log_2n- 1$ 或 $log_2n$ 或 $log_2n +1$
给定高度,最少节点数就只能通过递推得到,或者通过通项公式,最多节点数就是满二叉树的节点个数。
判断一棵二叉树是否为平衡二叉树,根据定义,我们有两种思路
- 计算节点总数和树的高度,从而确定树是否平衡(实际实践有难度,因为通项公式不容易求);
- 分别计算左右子树的深度,然后判断差是否为1
以第二种方法为例,代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| func isBalanced(root *TreeNode) bool {
if root == nil {
return true
}
t := height(root.Left) - height(root.Right)
if t > 1 || t < -1 {
return false
}
return isBalanced(root.Left) && isBalanced(root.Right)
}
func height(root *TreeNode) int {
if root == nil {
return 0
}
return max(height(root.Left), height(root.Right))+1
}
func max(a,b int) int {
if a > b {
return a
}
return b
}
|
3. 平衡二叉搜索树
平衡二叉搜索树的意义在于将针对二叉搜索树的算法复杂度限制到 O(logN),因为二叉搜索树的复杂度通常为O(h),最坏情况下,树成为链,树高将等于树中节点个数,我们将二叉搜索树调整为平衡的,就可以令树高最小,即 logN。
有许多方法可以实现平衡二叉搜索树,包括红黑树、AVL树、伸展树、树堆等。下面仅介绍 AVL 树,红黑树在后面的文章中介绍,不过在此之前,先介绍一个有意思的题型:将二叉搜索树变平衡。
3.1 将二叉搜索树变平衡
给你一棵二叉搜索树,请你返回一棵 平衡后 的二叉搜索树,新生成的树应该与原来的树有着相同的节点值。
该题当然不是要我们利用后面的 AVL 或红黑树,而是要重复利用二叉搜索树这一个条件。思路很简单,就是将二叉搜索树利用中序遍历变为递增序列,然后以中间节点为根结点重新构造二叉搜索树,这是一个贪心的思路。最后实现的代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func balanceBST(root *TreeNode) *TreeNode {
// 先中序遍历排序
if root == nil {
return root
}
var seqList []int
midOrder(root, &seqList)
// 然后用二分法分别构建左右子树
return build(0, len(seqList) - 1, seqList)
}
func midOrder(root *TreeNode, list *[]int) {
if root == nil {
return
}
midOrder(root.Left, list)
*list = append(*list, root.Val)
midOrder(root.Right, list)
}
func build(l, r int, list []int) *TreeNode {
if r < l {
return nil
}
mid := (l + r) >> 2
root := &TreeNode{Val: list[mid]}
root.Left = build(l, mid - 1, list)
root.Right = build(mid + 1, r, list)
return root
}
|
3.2 AVL树
AVL树是根据它的发明者G.M. Adelson-Velsky和E.M. Landis命名的,它是最先发明的平衡二叉查找树。
由于AVL树同样是一颗二叉搜索树,插入和删除的算法和二叉搜索树相同,但是插入和删除结点后,会造成树高和平衡因子的变化,从而不满足平衡二叉树的条件,因此需要对其进行调整。
以插入为例,将所有情况和对应的处理措施分为四种
RR
意为插入的结点在失衡点右子树的右子树中(左右孩子处理办法都一样),其解决办法是进行一次左旋转,如下图所示,14为新插入的结点。需要注意的是失衡点不一定是根结点。

简单的代码实现如下
1
2
3
4
5
6
7
8
9
| func leftRotate(root *TreeNode) *TreeNode {
tmp := root.Right
root.Right = tmp.Left
tmp.Left = root
root.Height = max(getHeight(root.Left), getHeight(root.Right)) + 1
tmp.Height = max(getHeight(tmp.Left), getHeight(tmp.Right)) + 1
return tmp
}
|
RL
意为插入的结点在失衡点右子树的左子树中(左右孩子都一样),其解决办法是先进行一次右旋转,再进行一次左旋转,如下图所示,插入结点分别为10.5和11.5

简单的代码实现如下
1
2
3
4
5
| func rightThenLeftRotate(root *TreeNode) *TreeNode {
tmp := rightRotate(root.Right)
root.Right = tmp
return leftRotate(root)
}
|
LL
意为插入的结点在失衡点左子树的左子树中(左右孩子都一样),其解决办法是进行一次右旋转,如下图所示,6为插入的新结点
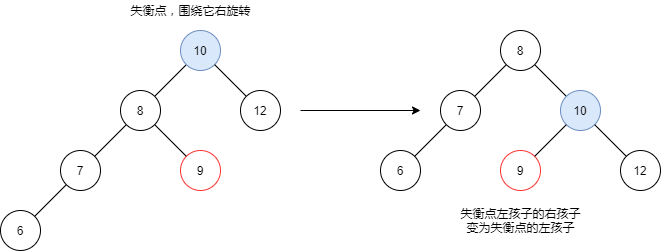
简单的代码实现如下
1
2
3
4
5
6
7
8
9
| func rightRotate(root *TreeNode) *TreeNode {
tmp := root.Left
root.Left = tmp.Right
tmp.Right = root
root.Height = max(getHeight(root.Left), getHeight(root.Right)) + 1
tmp.Height = max(getHeight(tmp.Left), getHeight(tmp.Right)) + 1
return tmp
}
|
LR
意为插入的结点在失衡点左子树的右子树中(左右孩子都一样),其解决办法是先进行一次左旋转,再进行一次右旋转,如下图所示,插入结点为8.5和9.5

简单的代码实现
1
2
3
4
5
| func leftThenRightRotate(root *TreeNode) *TreeNode {
tmp := leftRotate(root.Left)
root.Left = tmp
return rightRotate(root)
}
|
对于AVL树的所有操作都建立在这四个基本操作之上,在插入和删除操作完成后,调用调整函数,然后在调整函数中分情况调用这四个函数。调整函数的实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| func ajust(root *TreeNode) *TreeNode {
if root == nil {
return nil
}
compare := getHeight(root.Right) - getHeight(root.Left)
if compare == 2 {
if getHeight(root.Right.Right) > getHeight(root.Right.Left) {
root = leftRotate(root)
} else {
root = rightThenLeftRotate(root)
}
} else if compare == -2 {
if getHeight(root.Left.Left) > getHeight(root.Left.Right) {
root = rightRotate(root)
} else {
root = leftThenRightRotate(root)
}
}
return root
}
|
其中用到寻找最大值和获取高度两个工具函数,实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| func getHeight(root *TreeNode) int {
if root == nil {
return 0
}
return root.Height
}
func max(a int, b int) int {
if a > b {
return a
} else {
return b
}
}
|
4. 哈夫曼树
4.1 定义
设二叉树有 n 个叶子结点,每个叶子结点带有权值 wk,从根结点到每个叶子结点的长度位 lk,则每个叶子结点的带权路径长度(WPL)之和为:
$$
WPL = \sum_{k=1}^{n} w_k l_k
$$
WPL 最小的二叉树就叫做哈夫曼树(或者最优二叉树)。其特点有
4.2 构造
构造哈夫曼树的思路极为简单,即每次把权值最小的两棵二叉树合并,以{1,2,3,4,5}这组数为例,构造过程如下

其构造的关键在于每次寻找剩余结点中的最小值,最简单的实现是使用堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| type TreeNode struct {
Weight int
Left *TreeNode
Right *TreeNode
}
func Huffman(H MinHeap) {
//假设MinHeap类型已实现标准库中堆的相关接口,H已存好所有权值
var T TreeNode
heap.Init(H)
for i := 1; i < H.Len(); i++ {
T = TreeNode{}
T.Left = H.Pop(H)
T.Right = H.Pop(H)
T.Weight = T.Left.Weight + T.Right.Weight
H.Push(H, T)
}
T = H.Pop(H)
return T
}
|
4.3 哈夫曼编码
该问题的描述为:给定一段字符串,如何堆字符进行编码,可以使得该字符串的编码存储空间最少
例:假设有一段文本,包含58个字符,并由以下7个字符构成:a,e,i,s,t,空格(sp),换行(nl);这7个字符出现的次数不同,如何对这7个字符进行编码,可以使得总编码空间最少
如果用等长ASCII编码,则一共 58×8=464 位;如果用等长3位编码,则一共 58×3=174位;最后一种方法是不等长编码,即出现频率高的字符编码短,出现频率低的字符编码长。
使用不等长编码时,为了避免二义性,可以使用前缀码(prefix code),即任何字符的编码都不是另一字符编码的前缀。将二叉树用于编码,遵循下面的规则
假设四个字符的频率分别为:a-4, u-1, x-2, z-1,两个可用的编码树如下

按照构造哈夫曼树的方法,可以构造棵编码代价最小的二叉树,假设之前例子中的7个字符权值如上表,则可构造得到如下的哈夫曼编码树

参考资料
[1] CSDN-Golang实现平衡二叉树












 支付宝
支付宝 微信
微信